Derin öğrenmeye uzun bir giriş yaptıktan sonra işin kodlama kısmına geçme zamanımız geldi. Bu örnekte nöral ağ inşasını 13 adıma böldük. Bir bilgisayarın hatalardan öğrenme ve patern tanıma sürecine tanık olmaya hazırlanın. Başlıyoruz!
Dikkat: Bu yazı “Derin Öğrenmeye Genel Bakış” ve “Derin Öğrenmeye Genel Bakış – 2” yazılarının devamıdır. Konuyu anlamak için öncelikle bu yazıları okumalısınız.
Matriks ve Doğrusal Cebir Kavramları Üzerine Birkaç Söz
Aşağıdaki kodda matriks kelimesini göreceksiniz. Bu çok önemlidir. Matriks arabamızın motoru gibidir. Matriksler olmadan bir nöral ağ hiçbir yere gidemez.
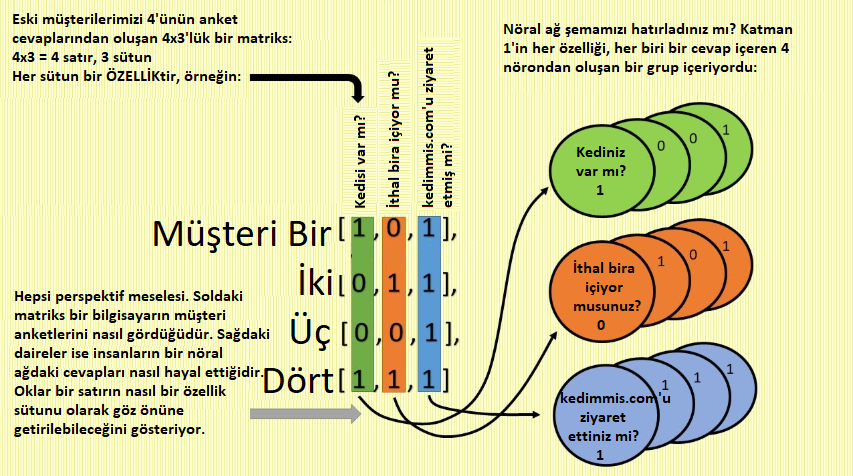
Matriks bir dizi sayı sırasıdır. Benzetme için Excel tablosunu düşünebilirsiniz. Ya da pek çok satır ve sütun içeren bir veritabanı hayal edin. Şimdi karşılaşacağınız ilk matriks ise evcil hayvan dükkanı anketimizdeki verileri içeriyor. Matriksimiz şuna benziyor:
[1,0,1],
[0,1,1],
[0,0,1],
[1,1,1]
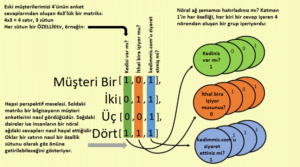
Her satırı bir müşteri gibi düşünün. Yukarıdaki matrikste dört müşteri vardır. Her satır üç sayı içeriyor. 1’ler evet, 0’lar hayır yanıtlarına karşılık geliyor. Daha önceki bölümde ilk müşterinin yanıtının “Evet/Hayır/Evet” olduğunu görmüştük. Bu matriksimizin en üst satırındadır. Birinci sütun dört müşterinin ilk anket sorusu olan “Kediniz var mı?” ya cevaplarını içeriyor (İki ve üç nolu müşterinin kedisi yoktur, bu nedenle sıfırla gösteriliyor). Şimdi biraz daha fazla ayrıntı göstermek için yukarıdaki matriksin aynısını şematize edelim.
Yukarıdaki şema müşteri satırları ile özellik sütunları arasındaki ilişkiyi anlamaya yardım etmiştir umarım. Matriksi her ikisi olarak da görmemiz gerekiyor. Şimdi parçalara ayıralım:
Matriksimizde bir müşterinin verisi üç numaralı bir satırla gösteriliyor. Birbirlerine çizgisel sinapslarla bağlanan dairesel nöronları içeren nöral ağ şemasında ise girdi katmanı üç dairesel “nöron”dan oluşmaktadır. Burada her bir nöronun bir müşteriyi – bir veri satırını temsil etmediğini bilmek önemlidir. Bunun yerine her nöron bir özelliği – veri sütununu temsil eder. Böylece bir nöron içinde tüm müşterilerin aynı soruya (örneğin “kediniz var mı?”) verdikleri cevaplara sahip oluruz. Sadece dört müşteriyi gösterdiğimiz için yukarıdaki şekilde o soruya karşılık gelen dört 1 ve 0’lar görmekteyiz. Ancak eğer 1.000.000 müşterinin çizelgesini çıkaracak olsaydık üstteki nöron her müşterinin “kediniz var mı?” sorusuna verdiği bir milyon 1 ve 0’lardan oluşan cevapları içerecekti.
Umarım matrikslere neden ihtiyacımız olduğu daha açık hale gelmiştir. Çünkü birden fazla müşterimiz var. Aşağıdaki nöral ağımızda dört müşteriyi tarif ettik, bu nedenle de dört sıra sayıya ihtiyaç duyduk.
Ağımızda birden fazla anket sorusu olduğu için her soruya (veya özelliğe) karşılık gelen bir sütuna ihtiyaç duyduk. Dördüncü soru ise farklı bir matrikste görünecektir. Bu kısma daha sonra değineceğiz.
Özetlersek matriksler karmaşık hesaplamalar yaparken verilerin düzenli durmasını sağlıyor.
Önemli not: Aşağıdaki kod sadece bir eğitim setini içeriyor. Doğrulama veya test setini içermiyor.
Aşağıda Python kodu arasına serpiştirilmiş yorumlar iyi bir özet olabilir ancak yine de karmaşıktır. Kodlama konusunda acemi olanlar ilk okuyuşta anlamayabilirler. Her şey ayrıntılı şekilde açıklanacaktır. Anlaşılmayan kısımların açıklaması yazının sonraki kısımlarında olabilir.
Kod
İlk önce koda çeki düzen verelim: Güçlü bir matematiksel araç olan numpy’i içe aktaralım.
import numpy as np
#1 Sigmoid Fonksiyon: Sayıları olasılıklara dönüştürür ve dereceli alçalma ile güvenilirliği hesaplar.
def nonlin(x,deriv=False):
if(deriv==True):
return x*(1-x)
return 1/(1+np.exp(-x))
#2 X Matriksi: Bu 4 müşterimize yaptığımız anketten aldığımız cevabın bilgisayarın anladığı dildeki halidir. Satır 1, birinci müşterinin ilk 3 anket sorusuna verdiği Evet/Hayır cevapları dizisidir:
“1”, “Kediniz var mı?”’ya Evet anlamına gelir. “0” “İthal bira içiyor musunuz?” sorusuna Hayır anlamına gelir. “kedimmis.com’u ziyaret ettiniz mi?” için 1, Evet anlamına gelir. Bunun altında 3 satır daha vardır (diğer 3 müşterinin cevapları için).
Yani bunlar 4 müşterinin ilk 3 soruya Evet/Hayır cevaplarıdır (4. soru aşağıdaki sonraki adımda kullanılmıştır).
Bunlar ağımızı eğitmek için kullanacağımız girdi setidir.
X = np.array([[1,0,1],
[0,1,1],
[0,0,1],
[1,1,1]])
#3 y vektörü: Dört hedef değer çıktımızdır. Bunlar 4 müşterinin dördüncü anket sorusu olan “Kedim Mis! satın aldınız mı?”ya verdikleri Evet/Hayır yanıtlarıdır. Nöral ağımız bir tahmin çıktısı verdiğinde bunu 4. soruya olan yanıtla, yani gerçekle karşılaştırırız. Ağımızın tahminleri bu 4 hedef değeri doğru yakaladığında yeterli doğruluğa ulaşmış demektir ve farklı bir veri setini almaya hazırdır. Örneğimizde ikinci veri setimiz veterinerden elde ettiğimiz anketlerdi.
y = np.array([[1],
[1],
[0],
[0]])
#4 Yerleştirme (seed): Bu ortama çeki düzen vermek gibi düşünülebilir. Sinapslarda eğitim sürecinde ürettiğimiz rastgele sayıları yerleştirmemiz gerekir. Bu hataları ayıklamayı kolaylaştırır.
np.random.seed(1)
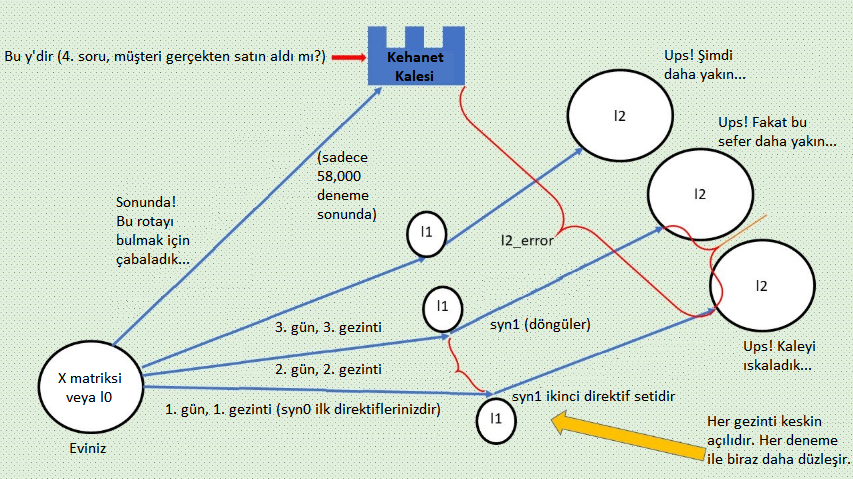
#5 Sinapslar: Diğer bir deyişle “ağırlıklar”. Bu iki matriks “beynin” tahmin yapan, deneme-yanılma ile öğrenen ve sonraki denemede kendini iyileştiren kısmıdır. Önceki yazılarda bahsettiğimiz eğri büğrü kırmızı kaseyi hatırlayın. syn0 ve syn1 kırmızı kasenin altındaki beyaz ızgaradaki X ve Y eksenleriydi. Böylece bu değerlere her ayar çektiğimizde ızgara koordinatlarını A noktasından kırmızı kasenin dibine yani hatanın sıfır olduğu yere doğru ilerletiriz (sarı okun hareketini düşünün).
syn0 = 2*np.random.random((3,4)) – 1 # Sinaps 0’ın 12 ağırlığı vardır ve l0’ı l1’e bağlar.
syn1 = 2*np.random.random((4,1)) – 1 # Sinaps 1’in 4 ağırlığı vardır ve l1’i l2’ye bağlar.
#6 Döngü için: Bu yineleyici ağımızı 60,000 tahmine, karşılaştırma ve iyileştirmeye götürür.
for j in range(60000):
# İleri besleme: l0, l1 ve l2’yi #5’teki sinaps matriksleri ile beraber tahmin eden, karşılaştıran ve iyileştiren 2 “nöron” matriks katmanı olarak düşünün. l0 veya X, 4 müşteri için kaydedilmiş anketimizin 3 özelliği/sorusudur.
l0=X
l1=nonlin(np.dot(l0,syn0))
l2=nonlin(np.dot(l1,syn1))
#8 Tahminlerimizi karşılaştıracağımız hedef değerler l2’dir. Böylece ne kadar ıskaladığımızı hesaplayabiliriz. y dördüncü soru olan “Kedim Mis! Satın aldınız mı?”ya 4 müşterinin verdiği cevapları içeren 4×1’lik bir vektördür. l2 vektörünü (ilk 4 tahminimiz) y’den (gerçek satın alma davranışları) çıkardığımızda l2_error’u elde ederiz. Bu tahminlerimizin belli bir denemede hedefi ne kadar ıskaladığını gösterir. Pratikte l2-error toplam hatanın bir türevidir (sıradaki yoruma bakın). Bu da l2_error karenin 2’ye bölümüne eşittir.
l2_error = y – l2
#9 Hatayı yazdır: 60,000 deneme içinde j’nin 10,000’le bölünmesi ile 6 kalır. Verimizi her 10,000 denemede bir kontrol ederek l2_error’un (A noktasında beyaz topun altındaki sarı okun yüksekliği) azalıp azalmadığına, yani her deneme ile hedef y değerini daha az ıskalayıp ıskalamadığımıza bakacağız.
if (j% 10000)==0:
Print(“10,000 ek deneme sonrası toplam hata: “+str(np.sum(np.abs(l2_error) / 2)))
#10 Bu geri yayılmanın başlangıcıdır. Takip eden basamakların tamamı tahminimizi iyileştirmek için syn0 ve syn1’deki ağırlıkları ayarlama hedefini paylaşır. Ayarlamamızı mümkün olduğunca verimli kılmak için ağırlıklarımızdaki en büyük hataları belirlemeliyiz. Bunun için ilk önce her l2 tahmininin eğimini alarak her l2 tahmininin güven düzeyini hesaplamalıyız. Ardından bunu l2_error ile çarpmalıyız. Başka bir deyişle l2_delta’yı belli bir değerin sigmoidindeki eğimle hatayı çarparak hesaplarız. Neden? Çünkü yüksek güvenli tahminlere (örneğin 0 veya 1’e yakın) karşılık gelen l2_error değerleri küçük bir sayı ile çarpılmalıdır (yüksek güvenliğe karşılık gelen düşük eğim), böylece az değişirler. Bu sayede ağımız en kötü tahminleri iyileştirmeye öncelik verir (örneğin 0.5’e yakın olan düşük güvenli tahminlerin daha dik eğimi olur).
l2_delta = l2_error*nonlin(l2,deriv=True)
#11 Geri yayılma devam ediyor. 7. adımda verimizi l0’dan l1 ve l2’ye, tahminimize ileri besledik. Şimdi geriye doğru çalışarak besleme yaptığımızda l1’in ne kadar hata içerdiğini bulacağız. l1_error en son hesaplanan l1 ile istediğimiz ideal l2’yi sağlayacak ideal l1 arasındaki farktır. l1_error’u bulmak için l2_delta’yı (bir sonraki denemede l2’nin olmasını istediğimiz hali) son denememizde en uygun olduğunu düşündüğümüz ağırlıklarla (syn1) çarpmalıyız. Başka bir deyişle syn0’ı güncellemek için syn1’in (mevcut değerleri ile) ağımızın tahminlerine etkilerini hesaba katmalıyız. Bunu l1_error’u veren yeni hesaplanmış l2_delta’nın sonucunu ve syn1’in mevcut değerini alarak yaparız. Bu da bir sonraki sefer l1’i değiştirmek için syn0’da yapacağımız güncellemenin miktarına karşılık gelir.
l1_error = l2_delta.dot(syn1.T)
#12 Yukarıdaki #10’a benzer şekilde orta tabaka l1’i ayarlayarak daha iyi bir l2 tahmini elde etmek istiyoruz. Böylece l2 y hedefini daha iyi öngörebilir. Yani düşük güvenli değerlerde ağırlıklarda büyük değişimler yaparken yüksek güvenli değerlerde küçük değişimler yaparız.
Bunun için #10’da olduğu gibi l1_error’u l1 değerindeki sigmoidin eğimi ile çarparız. Böylece ağ düşük güvenli (0.5’e yakın) tahminlerde sinaps ağırlıklarında daha büyük değişimler yapar.
l1_delta = l1_error * nonlin(l1,deriv=True)
#13 Sinapsları güncellemek: Bu dereceli alçalmadır. Bu adımda sinapslar, yani ağımızın gerçek beyni hatalarından öğrenir, hatırlar ve daha iyi olur. Her deltayı karşılık gelen tabaka ile çarparak bir sonraki denemede daha iyi tahmin yapmak için sinapslarımızı güncelleriz.
syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)
Sonuçları yazdırın!
print(“60,000 deneme sonrası y-l2 hata değerimiz: “)
print(l2)
Sigmoid Fonksiyon
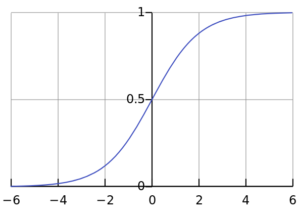
Satır 8’deki doğrusal olmayan (nonlineer) fonksiyon ağımızın öğrenmesinde çok önemli bir rol oynar. Ancak hepsini hemen kavrayamadıysanız korkmayın. Bu materyalin üzerinden ilk geçişimiz. Aşağıda 10. adımda daha ayrıntılı değineceğiz. Doğrusal olmayan fonksiyonun bir örneği olarak sigmoid fonksiyonu kullanacağız. Bugünlerde sigmoid ReLU’ya göre daha az kullanılıyor ancak sigmoidi öğrenmesi daha kolaydır ve sigmoidi anladıktan sonra ReLU fonksiyonunu kavramada zorlanmazsınız.
“nonlin()” lojistik fonksiyon denilen bir sigmoid fonksiyon tipidir. Lojistik fonksiyonlar bilimde, istatistikte ve olasılıkta çok yaygın kullanılırlar. Bu özel sigmoid fonksiyon burada gerektiğinden daha karmaşık yazılmıştır çünkü iki fonksiyona hizmet eder:
İki fonksiyondan ilki bir matriksi (burada küçük x ile temsil ediliyor) parantezine almak ve her bir değeri 0 ile 1 arasında bir sayıya (istatistiksel olasılığa) dönüştürmektir. Bu satır 12 ile yapılır: return 1/(1+np.exp(-x))
Neden istatistiksel olasılıklara ihtiyaç duyarız? Ağımızın sadece 0 ve 1’lerle öngörüde bulunmadığını hatırlayın. Ağımız “EVET! Birinci müşteri KESİNLİKLE Kedim Mis! alacak!” diye bağırmaz. Bunun yerine şunu der: “Birinci müşterinin Kedim Mis! alma olasılığı %74’dür.”
Bu önemli bir ayrımdır, çünkü 0 ve 1’lerle tahminde bulunursanız iyileştirmeye yer olmaz. Ya doğrusunuzdur ya yanlış. Ama olasılıkla beraber iyileştirmeye de yer açılır. Eğer her seferinde olasılığı doğru yönde birkaç ondalık hane iyileştirecek şekilde sisteme ayar çekmeniz mümkün olursa doğruluğunuzu arttırmaya devam edebilirsiniz.
Bunun önemini aşağıda daha iyi göreceğiz. Sıfır ile bir arasındaki bir sayıya dönüşüm bize dört büyük avantaj sağlar. Şimdilik sadece şunu bilin, sigmoid fonksiyon parantezindeki her matriksin her numarasını S-eğrisi üzerine düşen 0 ile 1 arasında bir sayıya dönüştürür. Bu aşağıda gösterilmiştir:
Böylece sigmoid fonksiyondaki Fonksiyon #1 matriksteki her değeri istatistiksel bir olasılığa dönüştürür.
Sigmoid fonksiyonun ikinci parçası Fonksiyon #2 9 ve 10. satırlardadır.
‘ if(deriv==True):
return x*(1-x) ‘
Kodun 9. satırında deriv=True ile yapması istendiğinde kod verilen bir matriksteki her değeri alır ve sigmoid S eğrisi üzerindeki belli bir noktanın eğimine dönüştürür. Eğim numarası aynı zamanda güven ölçümü olarak bilinir. Başka bir deyişle bu numara şu soruya cevap verir: “Bu numaranın bir sonucu doğru öngördüğünden ne kadar eminiz?” Yani? Amacımız güvenilir şekilde doğru tahminlerde bulunan bir nöral ağ oluşturmaktı. Bunu başarmanın en hızlı yolu güvenilir olmayan, boş, düşük doğruluktaki tahminleri düzelterek sadece doğru ve güvenilir tahminleri bırakmaktır. “Güven ölçümleri” kavramı çok önemlidir, birazdan değineceğiz. Şimdilik sadece bu boş ve güvenilmez sayıları aklınızda tutun.
X Girdisini Oluşturmak: 23-26. Satırlar
23-26. satırlar ağımızı eğitmekte kullanacağımız 4×3’lük girdi değerlerini oluşturur. X, ağımızda sıfır tabakası veya l0 (layer 0) olacaktır. Bu yarattığımız “oyuncak beyin”in başlangıcıdır.
Müşteri anketimizdeki özellik setini bilgisayarın anlayacağı dilde şöyle gösteririz:
Satır 23, X girdisini oluşturur (bu da satır 57’de 0 tabakası l0 olur)
x:
[1,0,1],
[0,1,1],
[0,0,1],
[1,1,1]
Üç sorumuza yanıt veren üç müşterimiz var. Yukarıdaki birinci satırın nasıl 101 olduğunu daha önce anlatmıştık. Bu birinci müşterinin anket sorularına verdiği Evet/Hayır cevaplarını gösteriyor.Bu matriksin her satırı ağımızı besleyeceğimiz bir eğitim örneğidir; her sütun da girdimizin bir özelliğidir. Böylece X matriksimiz aşağıdaki şekilde 4×3 matriks olarak l0 şeklinde şematize edilebilir.
X matriksinin nasıl olup da yukarıdaki şemada 0 tabakası (l0) olduğunu merak edebilirsiniz. Buna birazdan geleceğiz. Şimdi ağımızın tahmin edebilmesini istediğimiz dört doğru cevabın listesini oluşturalım.
y Çıktısını Oluşturmak: 34-37. Satırlar
Bunlar bizim çıktılarımızdır. Anketimizin dördüncü sorusu olan “Kedim Mis! satın aldınız mı?”nın cevaplarıdır. Aşağıda 4 sayıdan oluşan sütuna bakın. Burada birinci müşterinin evet, ikinci müşterinin evet şeklinde yanıt verdiğini göreceksiniz.
Satır 34 y vektörünü oluşturur; bunlar tahmin etmeye uğraştığımız değerlerdir.
y:
[1]
[1]
[0]
[0]
Benzetme yapmak için hedef y değerlerini bir hedef tahtası gibi düşünebiliriz. Ağımız iyileştikçe okları on ikiye gittikçe daha yakın fırlatır. Ağımız yukarıdaki X matriksindeki değerlerden hedef 4 değeri doğru şekilde tahmin edebildiğinde artık başka bir veritabanından (veterinerden elde ettiğimiz yeni anketlerden) tahmin yapmaya hazır demektir.
Rastgele Sayılar Yerleştirmek: Satır 40
Bu adımda sinapsları doldurmak için rastgele sayılar üretiriz. Nöronlar arasında korelasyondan kaçınmak için rastgele sayılarla başlarız. İdeal olarak her nöron farklı özellikleri öğrenmelidir. Rastgele sayı yerleştirme testlerimizi tekrar edilebilir kılar (örneğin aynı girdilerle çok sayıda test yaparsak sonuçlar aynı olur).
Rastgele sayı üretecini kullanarak eğitim sürecimizin bir sonraki adımı için gereken sinapsları / ağırlıkları üretecek rastgele sayıları oluştururuz. Böylece ayıklama işlemi kolaylaşır. Kodun nasıl çalıştığını anlamamız şart değildir, sadece eklememiz gerekir.
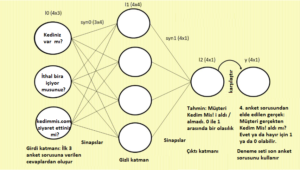
Beyin için Sinapsları – Ağırlıkları Oluşturmak: 47-48. Satırlar
Yukarıdaki şemaya bakınca ağın “beyni”nin daireler, nöral ağ beyninin “nöronları” olduğunu sanabilirsiniz. Gerçekte bir nöral ağın beyni, yani gerçekten öğrenen ve gelişen kısmı sinapslardır. Sinapslar şemada daireleri bağlayan çizgilerdir. Bu iki matriks, syn0 ve syn1, ağımızın beynidir. Bunlar ağımızın deneme-yanılma ile öğrenen, tahminlerde bulunan, hedef y değerleri ile kıyaslayan, ardından sonraki tahminlerini iyileştiren yani öğrenen kısımlarıdır!
Aşağıdaki
syn0 = 2*np.random.random((3,4)) – 1
Kodunun 3×4’lük bir matriks oluşturduğuna ve bunu rastgele değerlerle doldurduğuna dikkat edin. Bu l0’ı l1’e bağlayan sinapslarımızın veya ağırlıklarımızın, Sinaps 0’ın ilk tabakası olacaktır. Aşağıdaki matrikse benzer:
Satır 47: syn0 = 2*np.random.random((3,4)) – 1
Bu satır sinaps 0 veya syn0’ı üretir:
[ 0.36 -0.28 0.32 -0.15]
[-0.48 0.35 0.25 -0.25]
[ 0.16 -0.66 -0.28 0.18]
Şimdi, neden syn0 3×4’lük bir matriks olmak zorunda? l0 4×3 matriksi syn0’la çarpmamız gerektiği için mi? Böylece tüm sayıları satır ve sütunlara düzenli yerleştirebilelim diye mi? 4×3 ile 4×3’ü çarpmanın sayıları düzenli bir şekilde oluşturacağını düşünmek yanlıştır. Gerçekte eğer sayılarımız düzgünce sıralansın istiyorsak 4×3’ü 3×4 ile çarpmamız gerekir. Bu matriks çarpmanın temel ve önemli kurallarından biridir. Şimdi alıştığımzı şemadaki ilk nörona daha yakından bakalım. “Kediniz var mı?”
Bu nöronun içinde dört müşterinin her birinin verdiği Evet / Hayır cevapları vardır. Bu 4×3 tabaka0 (l0) matriksimizin ilk sütunudur:
[1]
[0]
[0]
[1]
“Kediniz var mı?” nöronunu l1’in dört nöronuna bağlayan dört çizgi (sinaps) olduğuna dikkat edin. Bunun anlamı yukarıdaki 1,0,0,1’in her birinin l1’deki “Kediniz var mı?” ya bağlanmak için dört farklı ağırlıkla dört kez çarpılması gerektiğidir. Böylece “Kediniz var mı?”nın içindeki dört sayı kere dört ağırlık = 16 değer eder, değil mi? Evet, l1 bu 4×4’lük matrikstir.
İkinci nöron olan “İthal bira içiyor musunuz?” içindeki dört sayı ile de tam olarak aynı şeyi yapacağımıza dikkat edin. Bu da dört ağırlık kere dört sayı = 16 değerdir. Biz de 16 değerin her birini yukarıda halihazırda oluşturduğumuz 4×4’te karşılık gelen değere ekleriz.
Son kez de üçüncü nöronun (“kedimmis.com’u ziyaret ettiniz mi?”) içindeki dört sayı ile tekrar ederiz. Böylece son 4×4 l1 matriksimizde 16 değer vardır ve bu değerlerin her biri az önce tamamladığımız üç çarpma setinden karşılık gelen değerlerin toplamıdır.
Şimdi anladınız mı? 3 anket sorusu kere 4 müşteri = 3 nöron kere 4 sinaps = 3 özellik kere 4 ağırlık = 3×4’lük bir matriks.
Karmaşık mı? Eğer bu konu üzerinde sabırla çalışırsanız alışacaksınız. Ayrıca çarpmaları sizin için bilgisayar yapar. Ancak kaputun altında neler olup bittiğini anlamamız önemlidir. Aşağıdaki gibi bir nöral ağ şemasına baktığımızda çizgiler yalan söylemez. Şunu düşünün:
Eğer “Kediniz var mı?” nöronunu sonraki tabakadaki dört nöronun tamamına bağlayan dört sinaps varsa, bunun anlamı “Kediniz var mı?”nın içinde olanı dört ağırlıkla çarpmanız gerektiğidir. Bu örnekte “Kediniz var mı?”nın içinde dört sayı olduğunu biliyoruz. Böylece 4×4’lük bir matriks elde edeceğimizi de biliyoruz. Buraya varmak içinse 3×4’lük bir matriksle çarpmamız gerekiyor: Örneğin 3 düğüm kere 4 sinaps her düğümü sonraki 4 nöronlu tabakaya bağlar. Aşağıdaki düzene iyice alışana, her sinapsın nerede başladığı ve bittiği sizin için açık olana kadar şemayı inceleyin:
Matriks çarpımının iç 2 “matriks büyüklüğü”nün eşleşmesini gerektirdiğini her zaman hatırlayın. Örneğin 4×3’lük bir matriks 3x_ ‘lük matriksle çarpılmalı. Bu örnekte 3×4’lük. İçteki iki sayı (bu örnekte 3) aynı olmalıdır.
Peki denklemimizin başındaki “2*” ve sonundaki “-1” nereden gelmektedir? np.random.random fonksiyonu rastgele sayıları 0 ve 1 arasında düzenli olarak yerleştirir (buna karşılık gelen ortalama 0,5’tir). Fakat bu başlatmanın ortalama sıfır olmasını istiyoruz. Neden? Çünkü bu matriksteki ilk ağırlık sayılarının 1 ya da 0’a yanlılığı olmamalı, çünkü bu henüz sahip olmadığımız bir güven verir (örneğin başlangıçta ağın ne olup bittiği hakkında fikri yoktur, bu nedenle her deneme ile güncelleyene kadar tahminlerinde güven sergilememelidir).
Peki ortalaması 0,5 olan bir dizi sayıyı 0 ortalamalı bir diziye nasıl çevirebiliriz? Önce tüm rastgele sayıları ikiyle çarparız (böylece 0 ile 2 arasında dağılımlı, 1 ortalamalı bir sonuç çıkar), ardından 1 çıkarırız (-1 ile 1 arasında 0 ortalamalı bir sonuç verir). Denklemimizin başındaki 2*’nin ve sonundaki -1’in nedeni budur. Böylece ortalama 0,5’ten 0’a iner. Güzel değil mi?
2*np.random.random((3,4)) – 1
Devam edelim. syn1 = 2*np.random.random((4,1)) – 1 kodu bir 4×1 vektör oluşturur ve bunu rastgele değerlerle doldurur. Bu ağımızın ikinci tabaka ağırlıkları, l1’i l2’ye bağlayan Sinaps 1 olur. Sinaps 1’le tanışın:
Satır 48: syn1 = 2*np.random.random((4,1)) – 1
Bu satır sinaps 1 veya syn1’i oluşturur:
[ 0.12]
[ 0.10]
[-0.63]
[-0.15]
Bu çarpma için matrikslerin hangi büyüklükte olması gerektiğini anlamak sizin için güzel bir egzersiz olabilir. syn1 Neden bir 4×1’dir? Şemaya bakın: l1’in en üstteki nöronunda olan sayılar sadece bir kez çarpılmalı, değil mi? Çünkü l1’in en üst nöronunu l2’deki tek nörona bağlayan sadece bir çizgi (ağırlık) vardır. l1’in en üstteki nöronunun dört değeri olduğunu biliyoruz ayrıca. Bu nedenle 4 değer x 1 ağırlık = dört sonuç. Bunları birbirine ekleyin ve bu size l2’nin içindeki ilk sonucu verir.
Bu işlemi l1’deki diğer 3 nöron için de 3 kere daha tekrar edin ve açıktır ki l2 bir 4×1’lik matrikstir (sadece tek bir sütun olduğunuda bir vektör olarak bilinir).
Tekrarlayalım: Her zaman içteki büyüklük numaralarının eşleşmesi gerektiğini hatırlayın. Bir 4×3’lük matriks bir 3x_’lık matriksle çarpılmalıdır. Bir 4×4’lük matriks 4x_’lık matriksle çarpılmalıdır gibi.
Döngü için: Satır 52
Bu ağımızı 60,000 denemeye sokacak döngü içindir. Her denemede ağımız X’i, müşteri anketlerimizdeki cevap verilerini alır, bu verilere göre o müşterinin Kedim Mis! alma ihtimali için en iyi tahminini yapar. Daha sonra tahminini y olarak bulunan gerçekle kıyaslar. Hatalarından öğrenerek bir sonraki denemesinde biraz daha iyi bir tahmin yapar ve bunu 60,000 kere tekrarlar. Ta ki deneme-yanılma ile X girdisinden y hedef değerini doğru şekilde tahmin edene dek. Böylece ağımız vereceğiniz herhangi bir girdi verisine hazır olacaktır (veterinerden temin ettiğiniz anketler gibi) ve hedefli reklamlarınız için uygun kişileri öngörebilecektir.
Burada süreci aslında basitleştirdik. Genelde hem bir eğitim seti hem de doğrulama seti kullanılır. Modellerini doğrulama seti hataları artana kadar, “erken durma” olarak adlandırılan yere kadar eğitirler. Burada öğretme amacıyla süreç basitleştirilmiştir.