Bu yazı “Derin Öğrenmeye Genel Bakış” başlıklı yazımızın devamıdır. Öncelikle o yazıyı okumanız gerekmektedir.
İleri Besleme: 1960’ların IBM Bilgisayarına Delikli Kartları Basmak
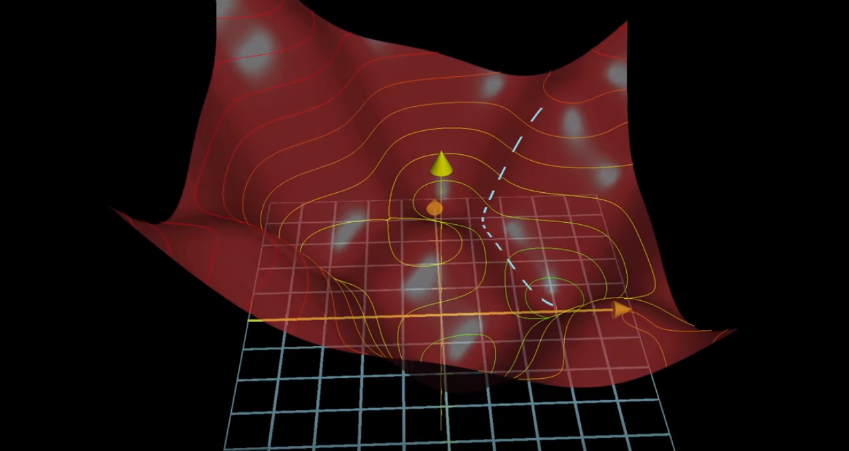
İleri beslemenin amacı bir tahminde bulunmaktır. Her tahmin, tahmin topunun kasenin kenarından hata içermeyen dip noktaya doğru giderken geçtiği yeni bir noktadır. Nöral ağın hangi müşterilerin kedi hijyen ürünü alacağına dair ilk tahmini kırmızı yumrulu kasedeki beyaz kesikli çizginin en üst noktasıdır. Tahmin topu yolculuğuna buradan başlar. İleri besleme tahmin topunun bulunduğu ilk tahmini üretme sürecidir. Kesikli beyaz çizgideki bir sonraki nokta ikinci tahmine karşılık gelir. Tahmin topu buraya doğru yuvarlanır. Ardından üçüncü tahmin gelir ve böyle devam eder.
Kırmızı yumrulu kasemiz uzay boşluğunda asılı değildir. X ve Y eksenlerine sahip bir alanda yer alır. Tahmin topunun konumu da bu koordinatlarla gösterilir.
Global minimumu tarif ederken kullandığımız basit kase bir masa üzerinde bulunmaktaydı. Bu kırmızı yumrulu kasenin X ve Y eksenlerinden oluşan ızgaranın üzerine oturması ile benzerdir. Beyaz ızgara, masa yüzeyini temsil ederken “mükemmel hatasız tahmin” ise kırmızı kasenin oturduğu yere karşılık gelir. Kasenin masa yüzeyi ile tek temas noktası kesikli beyaz çizginin aşağıda sona erdiği en dip kısımdır. Burası global minimumdur.
Tahmin topunun kırmızı kasedeki her durağı 3 koordinatla tanımlanır. X ve Y eksenleri ızgara (masa yüzeyi) üzerindeki yeri tanımlarken Z koordinatı tahmin topunun ızgaradan uzaklığını ifade eder.
Biraz kafa karıştırıcı olduğunun farkındayım. 3 boyutlu uzaydaki bu 3 koordinat gerçek hayatta ne anlama gelir?
Kırmızı yumrulu kasenin yüzeyindeki her kırmızı noktanın nöral ağın üç anket sorusunun belli ağırlıklandırılmış kombinasyonuyla yaptığı bir deneye karşılık geldiğini söylemiştik. Ağ bu deneyi nasıl yapar? Beyaz ızgaradaki X ve Y koordinatlarını kullanarak anket sorularının belirli bir kombinasyonunu temsil eden belirli bir yer önerir. X ve Y eksenleri esas olarak şunu sorar: “Hey, Z ekseni! Bu vurgu/ağırlık ile kombinasyon nasıl?” Z koordinatı bu belirli kombinasyonun ne derece hatalı olduğunu bize söyler. Z koordinatı hatayı ölçer.
Tekrar düşünelim. Kasenin tabanının, beyaz ızgaraya temas eden noktasının mükemmel doğru tahmin olduğunu söylemiştik. Böylece kasedeki her kırmızı nokta hatayı ifade eder. Kırmızı nokta beyaz ızgaradan uzaklaştıkça hata büyür.
Bu konu çok önemli olduğu için tekrar edelim. Beyaz ızgara ağın deneyebileceği her soru kombinasyonu ve vurgusunu temsil ediyor. Beyaz ızgaradaki her nokta için onun direkt yukarısındaki kırmızı nokta bu belirli kombinasyonun hata miktarını gösteriyor. Kırmızı kase aslında hata kasesidir. Sadece kasenin dibinde kırmızı noktanın beyaz ızgaraya temas ettiği yerde kırmızı nokta ile beyaz noktalar arasında mesafe bulunmaz ve hata yoktur.
Grafikteki koni şekilli sarı oka dikkat edin. Bu sarı ok Z eksenini temsil ediyor ve Z ekseni hatanın ölçüsüdür. Sarı okun ifade ettiği hata miktarı çok yararlıdır çünkü buradan öğrenerek bir dahaki sefere daha az hata yapmayı mümkün kılar.
Şimdi tahmin topunun kesikli beyaz çizginin her noktasında olduğunu ve sarı okun da her seferinde tahmin topunun altında yer alarak beraber hareket ettiğini hayal edelim. Top ağın yaptığı her bir tahmini temsil eder, Topun altındaki sarı ok ise tahmin topunun beyaz ızgaraya olan mesafesini ölçer. Yani her tahminin hatasını ölçer. Peki bu nasıl olur?
İleri besleme işleminin ilk üç anket sorusunu alıp bunları farklı şekillerde kombine ederek bir tahminde bulunduğunu, 0 ile 1 arasında bir olasılığı anlatan bir sayı ürettiğini söylemiştik. Tahmin topunun kesikli beyaz çizgide bir noktada bulunduğunu düşünelim. Dördüncü sorunun cevabının “evet” ya da 1 olduğunu biliyoruz yani gerçekte müşteri Kedim Mis! almış. Gerçek, global minimumdur yani tahminlerimizi iyileştirerek ulaşmak istediğimiz hedef, kırmızı kasenin beyaz ızgaraya temas ettiği noktadır. Böylece ağımız tahmin olasılığı sayısını 1’den çıkarır. İlk tahmin 0,5 ise müşterinin %50 olasılıkla ürünü satın aldığını gösterir. Sarı okun uzunluğu hata ölçümüdür. Bu örnekte 1 – 0,5 = 0,5’dir. Hata 0,5’dir (hata her zaman mutlak değerle ifade edilir, yani negatif değerde olamaz).
Aklınıza yattı mı? Dördüncü anket sorusu olmadan bir ağı eğitemezsiniz, çünkü tahminlerinizi karşılaştıracağınız bir gerçeğe ihtiyacınız vardır. Sarı ok ağın gerçeği ne ölçüde ıskaladığını, yani hatasını ölçer. İlk tahminimiz olan 0,5 pek doğru sayılmaz. Oysa ki 0,99 değerindeki bir tahmin gerçeğe çok daha yakın olduğu için daha doğru olurdu.
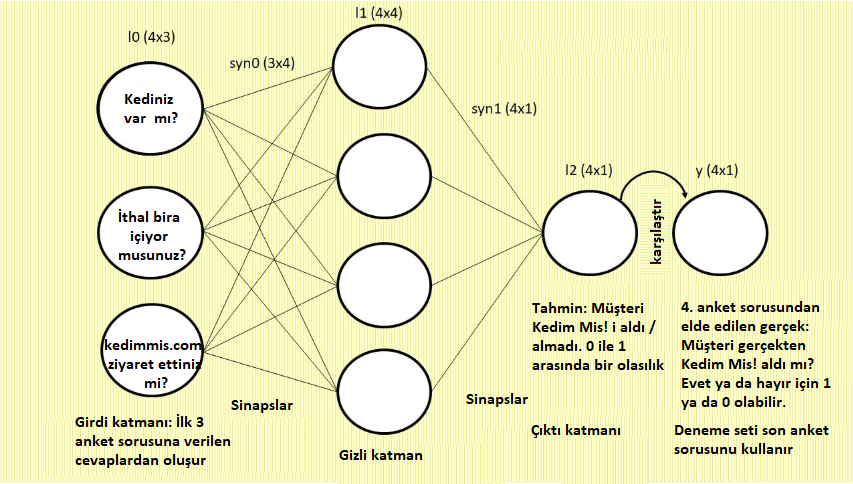
Şimdi belki ilk okumada hemen anlayamayacağınız bir bilgiyi paylaşalım. Izgara üzerindeki X ve Y eksenlerini temsil eden iki turuncu ok aslında daha sonra öğreneceğimiz syn0 ve syn1 sinapslarıdır. Şimdilik syn0’ın X ekseni ve 3’e eşit olduğunu, syn1’in Y ekseni ve 3’e eşit olduğunu söyleyelim.
İlk müşterinin ilk üç soruya verdiği Evet / Hayır / Evet cevaplarını anımsıyor musunuz? Ağımız ilk müşteri için 1, 0, 1 olarak bunları alır; syn0 ve syn1 sinapslarındaki sayılarla çarpar (ve başka bazı havalı şeyler yapar) ve bir tahminde bulunur. Bu tahminin 0,5 olduğunu söylemiştik. Bu bizim ilk ileri besleme tahminimizdir ve tahmin topumuzun kırmızı kase üzerindeki kesikli beyaz çizgide bulunduğu yerdir.
Global Minimumu Bulmak
Ağımızı eğitmemizin amacının tahminlerimizdeki hatayı en hızlı şekilde azaltmanın yolunu bulmak olduğunu söylemiştik. Başka bir deyişle sarı okun kısalmasını istiyoruz. Bunun için tahmin topumuzun başlangıç noktasından bükülmüş kasenin en dip noktasına (masaya temas ettiği noktaya) en verimli şekilde yuvarlanması gerekiyor. Buraya Ütopya diyebiliriz. Ütopyada tahminlerimizin hatasını ölçen Z ekseni uzunluk olarak neredeyse sıfırdır yani global minimumdur. Tahminlerimiz minimal hata içerir ve ağımız baş döndürücü doğruluktadır. Tahmin topumuzun eğimli kırmızı kasenin yüzeyinden yuvarlandığı en verimli rota kesikli beyaz çizgi ile temsil edilmiştir. İlk veri seti ile eğitimimizi tamamladığımızda ağımız veterinerden temin ettiğimiz potansiyel müşterilerden hangilerinin Kedim Mis! alma ihtimalinin en yüksek olduğunu doğru şekilde öngörebilir.
Şimdi şunu düşünelim: Tahmin topumuz kesikli beyaz çizginin en yukarısında başlıyor. Burada ilk tahminimizin hata payı 0,5’ti. Peki topu aşağıya yani hatanın sıfıra yaklaştığı yere doğru nasıl yuvarlayacağız? Ağımıza nasıl ince ayar çekeceğiz ki, şu anda X,Y koordinatı olarak (3,3) de bulunan tahmin topumuz kesikli beyaz çizgide ilerleyerek kasenin dibine, yaklaşık olarak (3,0) noktasına ulaşsın? Şimdiye kadar ilk müşterinin cevaplarına dayanarak tek tahminde bulunduk. Her bir müşterinin cevapları ile takip eden her bir tahminimizi nasıl iyileştirecek ve hata payımızı neredeyse sıfıra ulaştıracağız?
Kasenin dibine giden yolu adım adım bulmak, övünç kaynağı olmayan ilk tahminimiz 0,5’ten 60.000’inci tahmin sonrasındaki 0,9999 kesinliğine ulaşmak “dereceli alçalma” sürecidir.
Dereceli Alçalma ve Geri Yayılma
Dereceli alçalma bir ağın deneme-yanılma ile öğrenmesini anlatan süslü bir terimdir. Dereceli alçalma, her denemede hata miktarını azaltma amacıyla sinapsların ağırlıklarını değiştirmenin ana planıdır. Farklı şekilde tekrar ifade edilim: Tahmin topunu dip noktaya mümkün olduğunca çabuk ulaştırmak için en dik eğimli yolu takip etmek. Geri yayılma eğimi hesaplamak için kullanılan bir yöntemdir. Tahmin topunun altındaki kase yüzeyinin eğimini bize geri yayılma söyler.
Evet, her şey eğimle alakalıdır. “Dereceli alçalma” havalı bir terimdir fakat aslında sadece eğimi anlatır. Tahmin topumuzun oturduğu kase yüzeyinin eğimini bulmak topun yuvarlanması gereken yönü bize gösterir. Böylece hata payının sıfıra yaklaştığı dip noktaya en hızlı iniş sağlanabilir.
Şimdi dereceli alçalma sürecini düşünelim. İlk olarak bilgisayar ileri besleme tahminini yapar. Bu tahmini “gerçek”ten (global mimimumun bulunduğu tabandan) çıkarır ve hatayı (sarı okun uzunluğu) elde eder. Ardından geri yayılma hatanın eğimini hesaplamak için kullanılır. Eğim değeri tahmin topunun yuvarlanması gereken yönü ve hızı (ağdaki sayılarda ne kadar büyük ya da küçük ayarlama yapmak gerektiğini) belirler.
Eğimi bulmak geri yayılmada anahtar bir araçtır. Dereceli alçalma ana plan ise, geri yayılma bu plana ulaşmak için kullanılan esas araçtır. Biraz daha açalım:
Dereceli Alçalma Ana Plandır
Dereceli alçalma tam olarak ne yapar? Ağırlıkları değiştirerek her denemede tahminimizin hatasını azaltır.
Şimdiye kadar anket sorularının farklı kombinasyonları ve bu sorulara farklı vurgular ile mümkün olan en iyi tahmini gerçekleştirmek için ağın nasıl deney yaptığından bahsettik. Peki ağırlık nedir? Ağırlık tahmin için bir sorunun ne kadar önemli olduğunu belirleyen bir sayıdır. Bu oldukça önemli bir kavramdır. Ağırlıklar iki grup sinapsımızdaki değerlerdir (sayılardır). Ağ bu sinaps sayıları yani ağırlıkları ile oynayarak farklı soru kombinasyonları ve bu kombinasyonlar içindeki soruların vurgularını değiştirir ve deney yapar.
Sarı şemadaki nöronları bağlayan her çizgi bir sinaps veya ağırlıktır. Eğer bir ağırlığın değeri fazla ise “bu anket sorusunun ağın tahminine etkisi fazla” anlamına gelir. Başka bir deyişle bu anket sorusu doğru tahmin etmeye büyük katkı sağlar. Eğer ağırlık sıfıra yakınsa bu özelliğin/sorunun doğru tahminde bulunmakla fazla ilişkisi olmadığı anlamına gelir.
Geri Yayılma Dereceli Alçalmayı Başarmak için Ana Araçtır
Geri yayılma dereceyi (eğimi) hesaplamada kullandığımız yöntemdir. Bu derece bize sonraki denemede her ağırlığı yeniden ne kadar önceliklendirmemiz gerektiğini söyler. Tahmin topunun aşağı inerken kesikli beyaz çizgide uğradığı her nokta nöral ağın bir denemesi / tekrarıdır.
Peki deneme nedir? Bu çok önemli bir sorudur. Deneme-yanılma ile öğrenme sürecindeki bir denemedir. Denemenin ilk parçası ileri beslemedir. İleri besleme ile tahmin topumuz kesikli beyaz çizginin en üst kesimindeki başlangıç pozisyonuna yerleşir. Daha sonra buradan kırmızı kasenin yüzeyi boyunca dibe kadar yuvarlanır. Dipte hatanın neredeyse sıfır olduğu global minimum noktası vardır. Beyaz kesikli çizgideki her bir nokta ağın önerdiği anket soruları kombinasyonundaki bir güncelleme veya ayarlamayı temsil eder. Soruların ağırlıkları değiştirilerek biraz daha iyi bir tahminde bulunulabilir.
Tahmin topunun kıvrık kırmızı kase yüzeyi boyunca aşağı doğru izlediği rota düzensizdir. Top bazı tümseklerin üzerinden yuvarlanabilir, bazı vadilere inebilir, yönünü aniden değiştirebilir. Ne olduğunu anlamak için öncelikle dik ekseni oluşturan Z koordinatını düşünelim. Z koordinatını ifade eden sarı ok topla beraber, topun hemen altında hareket eder. Sarı okun boyunda pek çok değişiklik olur. Top kasenin tabanına yaklaştıkça sarı okun boyu kısalır ve sıfıra yaklaşır. Burada tahmin ile gerçek arasında fark neredeyse sıfırdır. Yani tahminlerimiz doğrudur. Sarı ok sıfıra eşit olduğunda X ve Y eksenleri kasenin hemen altında, global minimumda olmalıdır.
Şimdiye kadar evcil hayvan dükkanı müşterilerinin yaptığı basit bir anket ile bir nöral ağın kendini nasıl eğittiğini genel hatlarıyla açıklamaya çalıştık. Bundan sonraki aşama kaputu açarak deneme-yanılma süreci ile ağın öğrenmesini mümkün kılan kodları öğrenmek. Nöral ağın yaptığı şeyi üç boyutlu hayal edebilmek matematik ve kodlama ile yapılan şeyleri anlamamıza yardım edebilir. Eğer şimdiye kadar bahsettiğimiz kavramları tam olarak anlamamışsanız endişelenmeyin. Derin öğrenme karmaşık bir konudur ve bir okuma ile öğrenmeyi beklememelisiniz. Daha çok kavramı anlayıp farklı örnekler gördükçe anlayışınız gelişecektir.